Figuras geométricas principales

La geometría es una rama de las matemáticas encargada de estudiar las propiedades de las figuras en el plano o el espacio. Por eso hablamos de conceptos como puntos, rectas, planos, politopos (como paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.).

Además, la geometría es base teórica de la geometría descriptiva o del dibujo técnico, y sus aplicaciones son muchas: en la física aplicada, en mecánica, arquitectura, geografía, cartografía, astronomía, náutica, topografía, balística, etc., En realidad, la geometría lo impregna todo, incluyendo la preparación de diseños e incluso en la fabricación de artesanía.

En cuanto a las figuras geométricas, se trata de superficies delimitadas por líneas (curvas o rectas) o espacios delimitados por superficies. En el primer caso, nos encontramos ante polígonos, círculos, circunferencias, elipses… y, en el segundo, se trataría de poliedros.

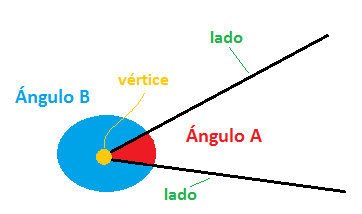
Así, un polígono sería una figura geométrica plana compuesta por una secuencia finita de segmentos rectos consecutivos que encierran una región en el plano. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices. En cuanto a los poliedros, se trata de cuerpos geométricos con caras planas que encierran un volumen finito. Son, por tanto, tridimensionales.

Estos son los principales tipos de figuras geométricas:

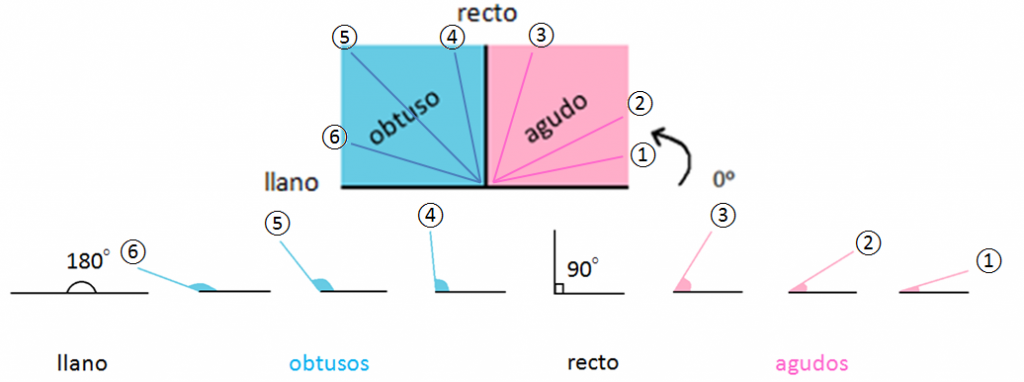
Triángulo. Se trata de un polígono formado por tres lados y tres ángulos. La suma de todos sus ángulos siempre es 180 grados. Para calcular el área se emplea la siguiente fórmula: Área del triángulo = (base x altura) / 2. Además, tenemos tres tipos de triángulos: isósceles, escaleno y equilátero.

Cuadrado. En el caso del cuadrado, se trata de un polígono de cuatro lados, siendo todos ellos iguales. Además, sus cuatro ángulos son de 90 grados. Su área se calcula mediante esta fórmula: Área del cuadrado = lado al cuadrado.

Rectángulo. El rectángulo es, al igual que el cuadrado, un polígono de cuatro lados, con la diferencia de que en este caso son iguales dos a dos. Sus cuatro ángulos son de 90 grados cada uno. El área de esta figura se calcula mediante la fórmula: Área del rectángulo = base x altura.

Rombo. El rombo es un polígono de cuatro lados iguales, pero sus cuatro ángulos son distintos de 90º. El área de esta figura se calcula mediante la fórmula: Área del rombo= (diagonal mayor x diagonal meno)/ 2.

Trapecio. En el caso del trapecio, se trata de un polígono de cuatro lados, pero sus cuatro ángulos son distintos de 90 grados. El área de esta figura se calcula mediante la fórmula: Área del trapecio = [(base mayor + base menor).altura] / 2.

Paralelogramo. En cuanto al paralelogramo, se trata de un polígono de cuatro lados paralelos dos a dos. Su área se calcula con esta fómula: Área del paralelogramo = base x altura.

Pentágono. El pentágono regular es un polígono de cinco lados iguales y cinco ángulos iguales. El área de esta figura se calcula con esta fórmula: Área del pentágono = (perímetro x apotema) / 2.

Hexágono. El hexágono regular es un polígono con seis lados iguales y seis ángulos iguales. Los triángulos formados son equiláteros, y el área de esta figura se calcula mediante la fórmula: Área del hexágono = (perímetro x apotema) / 2.

Círculo. Por último, el círculo es la región delimitada por una circunferencia, siendo ésta el lugar geométrico de los puntos que equidistan del centro. El área de esta figura se calcula mediante esta fórmula: Área del círculo = 3’14 x radio al cuadrado.

Click en el siguiente video para conocer mas sobre las figuras geométricas

Historia de la geometría

Para recordar la historia de la geometría, tenemos que remontarnos al segundo milenio a.C. en la zona de Egipto y Mesopotamia. La geometría básica ya se empleaba para calcular los volúmenes, los ángulos, los espacios y las longitudes, pero también se utilizaba de una manera más pragmática en los campos de la topografía, la construcción o la astronomía.

Durante el siglo VII a.C., el matemático griego Tales de Mileto comenzó a resolver distintos problemas matemáticos para calcular tanto la superficie de las pirámides como la distancia que separaba a los barcos de la costa.

Fue entonces cuando nació el famoso teorema de Tales, principio de la geometría muy enseñado en todas las escuelas de todo el mundo.

En la Edad Media, las matemáticas árabes contribuyeron en gran medida a la expansión de la geometría y al desarrollo de sus diferentes principios. Este período marcó el nacimiento de la geometría algebraica, un área de las matemáticas aplicadas, cuyo interés residía en el uso del álgebra para resolver problemas geométricos (curvas, espacios, etc.).

Finalmente, en las edades moderna y contemporánea, los matemáticos e inventores más ilustres, como René Descartes o Pierre de Fermat, desarrollaron la geometría no euclídea y la ciencia cuantitativa de la física y la química. Luego apareció la formación de la simetría durante el siglo XIX.

Los fundamentos de la geometría

Algunas nociones imprescindibles de geometría

Para saber reconocer una unidad de medida, aprender a representar en el espacio o a derivar, tendrás que familiarizarte con el ABC de la geometría.

En los libros de texto o durante la primera clase de geometría para principiantes, el alumno se enfrentará a los teoremas y principios más sencillos de esta rama de las matemáticas. No obstante, no te preocupes, con un poco de trabajo y una buena dosis de motivación, podrás aprender estas reglas básicas en tan solo unos meses.

Aquí te dejamos algunas reglas básicas indispensables de la geometría:

Vocabulario de las figuras: tangente, rectas paralelas, secantes, perpendiculares;

Ángulos: ángulo adyacente, ángulo opuesto, ángulo interno y externo, bisectriz;

Distancia: punto a punto, círculo y esfera, mediatriz, distancia ultramétrica, distancia de Hausdoff;

Plano cartesiano;

Triángulo isósceles, triángulo perpendicular, triángulo equilatero;

Teorema de Tales y teorema de Pitágoras...

Es un error común pensar que solo los doctorandos y los investigadores son capaces de llevar a cabo las teorías más complejas de la geometría. En realidad, la geometría es solo una cuestión de lógica: ¿por qué no desarrollas tu capacidad de reflexión a través de los juegos de lógica que hay en internet?

Los diferentes tipos de geometría

¿Quieres convertirte en un experto a la hora de representar gráficamente el espacio?

En el sentido estricto del término, hablamos de geometría para referirnos a la geometría clásica y euclídea que los profesores de matemáticas de todo el mundo enseñan en la escuela. En el instituto, a partir de Sexto de Primaria, los alumnos estudian conceptos simples de la geometría clásica que les permitirán introducirse en la representación gráfica más compleja.

Los alumnos podrán escoger diferentes campos de investigación de la geometría:

Geometría diferencial;

geometría algebraica;

geometría compleja;

geometría no conmutativa;

geometría no euclídea;

geometría aritmética;

geometría simpléctica y geometría de contacto;

geometría de Riemann...

Con la geometría denominada «clásica», en gran medida, te bastará para obtener una buena media en matemáticas.

No obstante, para convertirte en un verdadero «matemático» y continuar tu formación como profesor de matemáticas o maestro de Primaria, tendrás que tomar algunas clases complementarias sobre geometría teórica.

La elección de tu especialidad geométrica dependerá indudablemente de tus objetivos como matemático.

Puedes conocer mas acerca de la historia de la geometría en el siguiente video.

Propiedades de los ángulos

Imagina dos rectas en un plano. Hay dos posibilidades para dichas rectas: ya sea que se intersectan en cierto punto, o que nunca se intersectan. Cuando las rectas se intersectan, se forman cuatro ángulos. Entender cómo estos ángulos se relacionan unos con otros puede ayudarte a encontrar sus medidas, incluso cuando conoces la medida de sólo uno de ellos.

Paralelo y perpendicular

Las rectas paralelas son dos o más rectas que se intersectan. De la misma forma, los segmentos de recta paralelos son dos segmentos de recta que nunca se intersectan, incluso si los segmentos se convierten en rectas y continúan por siempre. Hay muchos ejemplos de rectas paralelas alrededor, en los dos lados de ésta página y en los estantes de un librero. Cuando ves que rectas o estructuras siguen la misma dirección, nunca se cruzan unas con otras, y mantienen la misma distancia entre ellas, es muy probable que sean paralelas.

Las rectas perpendiculares son dos rectas que se intersectan formando un ángulo recto (90º). Y segmentos de recta perpendiculares también se intersectan a 90º. También podemos ver ejemplos de rectas perpendiculares en todos lados — en la cuadrícula de un cuaderno, en el patrón de calles que se intersectan, las líneas de colores de una camisa a cuadros. En nuestras vidas diarias, podrías llamar perpendiculares a cualquier par de rectas que parecen intersectarse en ángulo recto. Sin embargo, cuando estudiamos geometría, necesitas asegurarte que las rectas se intersectan exactamente a 90º antes de declararlas perpendiculares.

La imagen siguiente muestra algunas rectas paralelas y perpendiculares. El símbolo geométrico para paralelo es , por lo que puedes tener . Las rectas paralelas también se pueden indicar con las marcas >> en cada recta (o sólo una marca > en cada recta). Las rectas perpendiculares se identifican con el símbolo , por lo que podemos escribir .

Ejemplo

Problema: Identificar un conjunto de rectas paralelas y un conjunto de rectas perpendiculares en la imagen siguiente.

Ejemplo

Problema

Identificar un conjunto de rectas paralelas y un conjunto de rectas perpendiculares en la imagen siguiente.






Las rectas paralelas nunca se encuentran, y las rectas perpendiculares se intersectan formando un ángulo recto.
y no se intersectan, pero si imaginas que se extienden, se intersectarán pronto. Entonces, no son ni paralelas ni perpendiculares.



es perpendicular a y a , como lo indica la marca de esquina en su intersección.



Como es perpendicular a ambas rectas, entonces y son paralelas.

Respuesta

En el siguiente video se explica mas sobre las propiedades de los ángulos

¿Qué son los ángulos?

¿Qué es un ángulo?

Un ángulo es la porción del plano comprendida entre dos semirrectas que tienen un origen común. El ángulo es el arco que se forma a partir de la cruce de dos semirrectas, segmentos o rectas, pudiendo ser medido en grados (con el sistema sexagesimal) o en radianes.

Partes de un ángulo

En un plano, dos semirrectas con un origen común siempre generan dos ángulos.

En el dibujo podemos ver dos, el A y el B.

Están compuestos por dos lados y un vértice en el origen cada uno.

Tipos de ángulos

Hay varios tipos según su tamaño, es decir, en función de los grados que tenga:

Ángulo agudo: Mide menos de 90° y más de 0 °.

Ángulo recto: Mide 90° y sus lados son siempre perpendiculares entre sí. En esta entrada del blog puedes aprender todo sobre los ángulos rectos.

Ángulo obtuso: Mayor que 90° pero menor que 180°. Para saber todo sobre el ángulo obtuso, revisa este post del blog de Smartick.

Ángulo llano: Mide 180°. Igual que si juntamos dos ángulos rectos. Si quieres aprender más sobre ángulos llanos puedes leer este post de nuestro blog.

Con una imagen lo verás más fácil. Todo ángulo comprendido en la zona rosa es un ángulo agudo, y todo ángulo comprendido en la zona azul es un ángulo obtuso.

Ejemplos de ángulos en la vida cotidiana

A continuación veremos algunos ejemplos de ángulos en nuestra vida cotidiana.

En el cono del helado y en la separación de los siguientes dedos tenemos ángulos agudos, ya que su abertura es menor de 90º.

En la posición de los siguientes dedos en forma de L y en la esquina del corcho podemos observar los ángulos de 90°, rectos.

La apertura del abanico es mayor que 90° y menor que 180°, por lo cual tenemos un ángulo obtuso.

Y por último tenemos un brazo estirado formando un ángulo llano de 180°.

Ejercicios de ángulos

A continuación te dejamos varios ejemplos de ángulos que forman las agujas de un reloj. Escríbenos en comentarios y dinos qué tipo de ángulo es cada uno de ellos.

Presione clic en el siguiente video para conocer sobre los ángulos:

Funciones: qué son, concepto y tipos

¿Qué son las funciones?

En matemáticas se conoce que las funciones son esa relación que existe entre el dominio, que llega a ser un conjunto conocido como X y el codominio que llamaremos A cada uno de los elementos x le corresponde o se le debe asignar un elemento único f(x) que son los que le dan forma al rango o, mejor dicho, al ámbito. Para explicarlo de una forma más simple se puede decir que las funciones consisten en una relación que se crea entre dos magnitudes. Esto establece que el valor que tiene la primera es el mismo que debe tener la segunda.

La manera de ilustrar un conjunto de funciones es a través de un diagrama donde se implementan también el uso de flechas que sirven para la forma que se van asociando los elementos de cada conjunto. Esta no es la única manera ya que se puede ilustrar también con una tabla de valores, con expresiones algebraicas o usando las gráficas. El uso de una ilustración u otra va a depender de lo que se desee representar pues hay algunas que pueden funcionar de mejor manera.

Tipos de funciones

Existen diferentes tipos de funciones, su clasificación va de acuerdo a el comportamiento que presente. Además se toma en cuenta la relación que se pueda establecer entre sus variables. 

Funciones algebraicas

Las funciones algebraicas son todo un conjunto de funciones cuya característica más notable es que establecen una relación. Esta se puede componer de monomios o polinomios. Las relaciones se hacen evidentes en operaciones que se consideran básicas como la suma, la resta y algunas más. Dentro de este tipo de funciones existen las siguientes:

Funciones explícitas: Son aquellas funciones que tienen una relación que se obtiene de forma directa al sustituir el dominio X por el valor correspondiente. Es decir que la función explícita es en la que se encuentra la igualdad entre los valores de Y y la relación correspondiente al dominio X directamente.

Funciones Implícitas: Este tipo de funciones son aquellas en las que para dar con la relación existente entre el dominio y codominio, se necesita realizar algunas operaciones que implican el uso de polinomios pero de diferentes grados. En este tipo de funciones están las funciones de identidad en las que se ve una identificación clara entre el codominio y el dominio siendo los valores siempre iguales. Las funciones cuadráticas son aquellas en las que se introducen los polinomios donde la variable se comporta de manera no lineal. En el caso de las constantes que tienen un número real único que es el determinante que define la relación entre el dominio y codominio.

Funciones racionales: Son ese conjunto de funciones en las cuales se establece un cociente entre los polinomios que son diferentes de cero.

Funciones Irracionales: Son aquellas en las que se ve a una función racional que aparece dentro de una raíz.

Funciones definidas a trozos: Son esas en las que se ve que el valor de Y puede que cambie el comportamiento de las funciones.

 
Funciones trascendentales

Se conoce con el nombre de funciones trascendentales a aquellas en las que existen representaciones matemáticas que tienen una relación entre las diferentes magnitudes. Estas no se pueden obtener por medio de operaciones algebraicas sino que es necesario hacer un proceso. Esto puede resultar algo complicado de cálculos con el que se obtiene esa relación. En estas se debe incluir las funciones que necesitan el uso de derivadas, logaritmos, integrales y todo lo que implica un crecimiento. Puede que este crecimiento sea hacia arriba o hacia abajo y de manera continua. Dentro de estas funciones se encuentran:

Si quieres conocer mas sobre las funciones observe el siguiente video.

Los 10 Casos de Factorización

Factor común.
Factor común por agrupación de términos.
Trinomio cuadrado perfecto.
Diferencia de cuadrados.
Trinomio cuadrado perfecto por adición o sustracción.
Trinomio de la forma X^2 + BX + C
Suma o diferencia de potencias.
Trinomio de la forma aX^2 + bX + c.
Suma y diferencia de cubos.
Raíces de un polinomio.

Caso #1 - Factoreo por factor común

Cuando en los diversos términos de un polinomio participa un mismo factor, se dice que se le saca como factor común, para lo cual, se escribe e inmediatamente, después, dentro de un paréntesis se anotan los cocientes que resulten de dividir cada uno de los términos del polinomio entre el factor común.

Ejemplo:

Otros ejemplos: a) 8X + 2Y = 2 * (4X + Y) (En este caso el factor común es 2)

b) a2 + 2a = a(a+2)

c) 10b + 30ab2 = 10b(1 + 3ab)

d) 10a2 + 5a + 15a3 = 5a(2a + 1 + 3a2)

e) 5a3b2x + 15a4bx2 − 35a2b2x4y5 = 5a2bx(ab + 3a2x − 7bx3y5 )

Caso #2 - Factoreo por agrupamiento

Algunas veces en un polinomio los términos no contienen ningún factor común, pero pueden ser separados en grupos de términos con factor común.

Este método consiste en formar grupos, los más adecuados, para factorizar cada uno como más convenga en cada caso y lograr finalmente la factorización total de la expresión.

Ejemplos: Factorizar:

a) 5a + 5b + ax + bx . Agrupando los términos que tengan algún factor común se tiene: 5(a+b)+ x(a+ b) = (a +b)(5 + x) o también a(5+ x)+ b(5+ x) = (a +b)(5 + x)

b) x2 +ax+bx+ab= x(x+a)+b(x+a)=(x+a)(x+b)

c) 8ax−bx+8ay−by) =8a(x+y)−b(x+y)=(x+y)(8a −b)

Caso #3 - Factoreo por Trinomio cuadrado perfecto.

En este caso se tiene un polinomio de grado dos y cuyas raíces están en el campo de los números reales, por ejemplo.

X^2 ± 2*a*X + a^2 = (X ± a)^2

Caso #4 - Factoreo por fiferencia de cuadrados.

Este es el caso de un producto de dos binomios cuya diferencia es solo el signo del segundo término.

(a + b) * (a – b) = a^2 – b^2

Caso #5 - Factoreo por Trinomio cuadrado perfecto por adición o sustracción.

Este caso ocurre cuando se posee un trinomio cuadrado perfecto en el que no es posible obtener dos raíces iguales y en el campo de los números reales. Se suma y resta la cantidad necesaria para obtener la forma del trinomio deseado.

X^2 + 2X – 5 = (X^2 + 2X + 2) – 2 – 5 = (X + 1)^2 – 7

Caso #6 - Factoreo por Trinomio de la forma X^2 + BX + C

En este caso de factorización se tiene un trinomio que tiene raíces reales pero que no son ni repetidas ni siguen el del caso anterior. Para ello se deben conseguir las raíces del polinomio.

X^2 – 5X + 6 = (x – 3) * (x + 2)

Caso #7 - Factoreo por Suma o diferencia de potencias.

Se trata de descomponer factores que compartan una misma potencia.

X^3 + 27 = X^3 + 3^3 = (X + 3) * (X^2 – 3X + 9)

Caso #8 - Factoreo por trinomio de la forma aX^2 + bX + c.

Para este caso se puede factorizar utilizando la ecuación de la resolvente la cual es la siguiente:

X = - b ± √b^2 – 4*a*c / 2*a

4X^2 + 12X + 9

X = - 12 ± √(12)^2 – 4*4*9 / 2*4

X1 = X2 = -1,5

4X^2 + 12X + 9 = (X + 1,5) * (X + 1,5)

Caso #9 - Factoreo por Suma y diferencia de cubos.

Son de la siguiente forma:

a^3 ± b^3 = (a ± b) * (a^2 ± a*b + b^2)

Caso #10 - Factoreo por raíces de un polinomio.

Mas información referente a los casos de factoreo en el siguiente video.

Importancia de los polinomios en la vida cotidiana

Los polinomios son una combinación de varios términos que pueden sumarse, restarse o multiplicar pero no divididos. Son una de las operaciones algebraicas básicas, y muchos estudiantes de álgebra pueden preguntarse por qué tienen que molestarse en aprender acerca de ellos. Mientras los polinomios están en aplicaciones sofisticadas, también tienen muchos usos en la vida cotidiana.

Planeamiento financiero

Los polinomios pueden ser utilizados en la planificación financiera. Por ejemplo, una ecuación polinómica se puede utilizar para calcular la cantidad de interés que se devengará de una cantidad de depósito inicial en una inversión o cuenta de ahorros a una tasa de interés dada. Si una cuenta de ahorros con un depósito inicial de US$3.000 gana interés del 3 por ciento, entonces esta ecuación polinómica demuestra el interés ganado por tres años: Interés=(3000)(3%)(3). En esta situación, la cuenta de ahorro acumularía US$270 de intereses durante los tres años.

Construcción o planeamiento de materiales

Los polinomios se aplican a los problemas de la construcción o la planificación de materiales. Una ecuación polinómica se puede utilizar en cualquier situación de la construcción 2-D para planificar la cantidad de materiales necesarios. Por ejemplo, los polinomios pueden ser usados ​​para determinar la cantidad de área de superficie de un jardín que puede ser cubierto con una cierta cantidad de suelo. El mismo método se aplica a muchos proyectos de la superficie plana, incluyendo calzada, acera y la construcción del patio.

Presupuesto de gastos

Los polinomios son útiles cuando se trata de presupuestos o la planificación de gastos. Cuando necesitas obtener una determinada cantidad de dinero dentro de un cierto período de tiempo, los polinomios pueden ayudarte a determinar la cantidad exacta de tiempo que necesitas para ganar esa cantidad. Al predecir tus gastos y saber tu tasa de ingreso, puedes fácilmente determinar la cantidad de tiempo que necesitas trabajar. Si necesitas ganar US$4.000, puedes ganar US$350 por semana con tus gastos totales de US$75 por semana, entonces la ecuación es 350x-75x=4.000, donde x es la cantidad de semanas necesarias para trabajar. La solución de la ecuación es 14 1/2, lo que significa que tendrías que trabajar 14 1/2 semanas con el fin de ahorrar US$4.000.

Aceleración gravitacional

Los polinomios se utilizan también en los problemas científicos, entre ellos problemas de aceleración gravitacional. La ecuación polinómica debe incluir la posición del objeto inicial, que es la distancia desde el centro de la Tierra, su velocidad inicial y su aceleración debida a la gravedad, que es una figura constante. La aceleración estándar aceptada de gravedad es 32,17 pies por segundo al cuadrado (9,8 m/s2). Esa es una fórmula básica, y muchos otros aspectos tales como la resistencia del aire o de la densidad del aire son factorizados por un científico que busca una solución altamente específica.

Si desea conocer mas sobre la importancia de los polinomios de click en el siguiente video